조합 논리는 논리 게이트로 구현되며 조합 논리에서 출력은 현재 입력의 함수입니다. 디자이너의 목표는 최소한의 논리 게이트 또는 논리 셀을 사용하여 논리를 구현하는 것입니다. 최소화 기법은 K-map, Boolean algebra, Shannon의 확장 정리입니다.
디자이너의 사고 과정은 디자인이 더 적은 논리 밀도로 더 나은 성능을 갖도록 해야 합니다. 면적 최소화 기술은 조합 논리 또는 부울 함수의 설계에서 중요한 역할을 합니다.
구성의 역할
조합 논리를 모델링하기 위해 할당 및 always @ 구문을 사용합니다. Always procedural 블록 내에서 if와 else로 구성하고 대부분의 경우 멀티플렉서 종류의 논리를 추론합니다.
if-else는 순차 구조이고 구문은 다음과 같습니다.
if (condition)
//blocking assignment executed if condition is true
else
// blocking assignment is executed if condition specified in if () is false
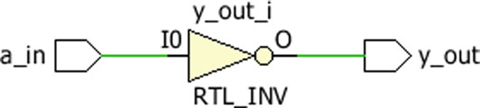
NOT 또는 논리 반전
NOT 논리는 반전 논리라고도 합니다.
합성 가능한 설계는 다음 예제와 같다.
module not_gate( input a_in, output reg y_out);
always@(a_in)
begin
y_out = ~a_in;
end
endmodule
module not_gate( input a_in, output y_out);
assign y_out = ~a_in;
endmodule
NOT 게이트의 진리표
| a_in | y_out |
| 0 | 1 |
| 1 | 0 |
OR 논리
OR 논리는 입력 중 하나가 논리 1일 때 논리 1로 출력을 생성합니다.
OR 게이트 진리표
| a_in | b_in | y_out |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
module or_gate(input a_in, b_in , output reg y_out);
always@(a_in, b_in)
begin
if ( a_in==0 && b_in ==0)
y_out = 0;
else
y_out = 1;
end
endmodule
다음 그림은 OR 논리의 RTL 개략도이며, OR 논리 게이트의 입력 포트는 a_in, b_in, 출력 포트는 y_out입니다. 회로도에서 볼 수 있듯이 추론된 논리는 2:1 멀티플렉서 및 기타 연산자를 사용하여 논리를 추론합니다. 합성 결과는 EDA 도구에 따라 다르며 ASIC 및 FPGA 설계의 경우 합성 결과가 다를 수 있습니다.
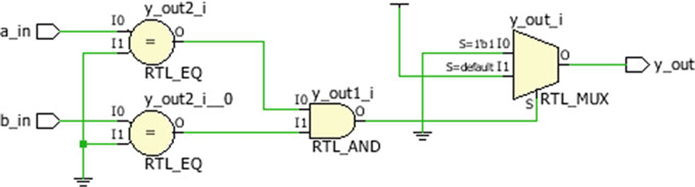
다중 입력 OR 게이트의 경우 비트 연산자( | )를 사용할 수 있습니다.
module or_gate(input [7:0] a_in, b_in , output [7:0] y_out);
assign y_out = a_in | b_in;
endmodule

NOR 논리
NOR 논리는 OR 논리의 반전입니다.
NOR 논리의 진리표
| a_in | b_in | y_out |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
module nor_gate(input a_in, b_in , output reg y_out);
always@(a_in, b_in)
begin
if ( a_in==0 && b_in ==0)
y_out = 1;
else
y_out = 0;
end
endmodule
NOR 논리 게이트의 입력 포트는 a_in, b_in, 출력 포트는 y_out입니다. 그림과 같이 추론된 논리는 등호 연산자와 AND 게이트를 사용하여 NOR 게이트를 구현합니다.
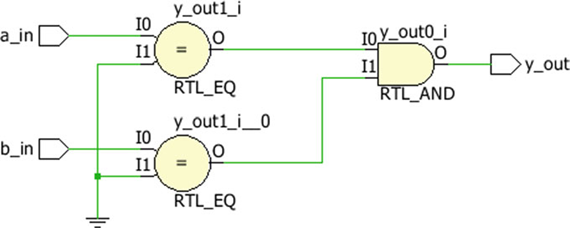
다중 입력 OR 게이트의 경우 비트 연산자 OR( | )의 비트 NOT(~)을 사용할 수 있습니다.
module nor_gate(input [7:0] a_in, b_in , output [7:0] y_out);
assign y_out = ~(a_in | b_in);
endmodule

AND 논리
AND 논리는 입력 a_in, b_in이 모두 논리 1일 때 논리 1로 출력을 생성합니다.
AND 논리의 진리표
| a_in | b_in | y_out |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
module and_gate(input a_in, b_in , output reg y_out);
always@(a_in, b_in)
begin
if ( a_in==1 && b_in ==1)
y_out = 1;
else
y_out = 0;
end
endmodule
낸드 로직
NAND는 AND 논리의 반전입니다.
NAND 논리의 진리표
| a_in | b_in | y_out |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
module nand_gate(input a_in, b_in , output reg y_out);
always@(a_in, b_in)
begin
if ( a_in==1 && b_in ==1)
y_out = 0;
else
y_out = 1;
end
endmodule
NAND 로직의 RTL 회로도는 다음 그림과 같으며, NAND 로직 게이트의 입력 포트는 a_in, b_in으로 명명되고 출력은 y_out으로 명명됩니다. 추론된 논리는 멀티플렉서를 사용하여 AND의 NOT을 생성합니다.

다중 입력 NAND 게이트는 할당 구성을 사용하고 비트 NOT(~) 및 비트 AND(&) 연산자가 있는 표현식을 사용하여 코딩되며 다음 예제와 같습니다.
module nand_gate(input [7:0] a_in, b_in , output [7:0] y_out);
assign y_out = ~(a_in & b_in);
endmodule

2입력 XOR 논리
두 개의 입력 XOR을 배타적 논리합(exclusive OR logic)이라고 하며 두 입력이 같지 않을 때 논리 1로 출력을 생성합니다.
XOR 논리의 진리표
| a_in | b_in | y_out |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
module xor_gate(input a_in, b_in , output reg y_out);
always@(a_in, b_in)
begin
if ( a_in != b_in )
y_out = 1;
else
y_out = 0;
end
endmodule
다중 입력 XOR 게이트에 대한 RTL은 비트 단위 연산자를 사용하여 코딩됩니다.
module xor_gate ( input [7:0] a_in, b_in , output [7:0] y_out );
assign y_out = (a_in ^ b_in);
endmodule
2입력 XNOR 논리
두 개의 입력 XNOR를 배타적 NOR 논리라고 하며 두 개의 입력이 같을 때 논리 1로 출력을 생성합니다. XNOR는 XOR 논리의 반전입니다.
module xnor_gate(input a_in, b_in , output reg y_out);
always@(a_in, b_in)
begin
if ( a_in == b_in )
y_out = 1;
else
y_out = 0;
end
endmodule
라이브러리에서 XNOR 게이트를 사용할 수 없는 경우 AND-OR-invert를 사용하거나 최소 수의 NAND 또는 NOR 게이트를 사용하여 XNOR 논리를 실현할 수 있습니다.
다중 입력 XNOR에 대한 RTL은 다음 예제와 같습니다.
module xnor_gate(input [7:0] a_in, b_in , output [7:0] y_out);
assign y_out = (a_in ~^ b_in);
endmodule
tri-state 논리
Tristate에는 논리 0, 논리 1 및 고임피던스 z의 세 가지 논리 상태가 있습니다.
tri-state 버퍼 논리의 진리표
| Enable | data_in | data_out |
| 1 | 0000 | 0000 |
| 1 | 1111 | 1111 |
| 0 | xxxx | zzzz |
module tri_state_logic ( input [3:0] data_in, input enable, output reg [3:0] data_out );
always@(data_in, enable)
begin
if (enable)
data_out = data_in;
else
data_out= 4'bZZZZ;
end
endmodule
'프로그래밍 언어 > Verilog' 카테고리의 다른 글
| [Verilog 학습] 다중비트 가산기 및 감산기 (0) | 2022.04.09 |
|---|---|
| [Verilog 학습] Verilog 산술 회로 (0) | 2022.04.08 |
| [Verilog 학습] Verilog 연산자 3 (0) | 2022.04.06 |
| [Verilog 학습] Verilog 연산자 2 (0) | 2022.04.05 |
| [Verilog 학습] Verilog 연산자 1 (0) | 2022.04.04 |